This article is a short journey to the theme ‘risk management’ as we are often asked…
How high should be a starting bank?
Is 5,000 units enough?
Well, there is no standard answer to this question. It all depends on the individual strategy.
 Image: Sergey Novikov (Shutterstock)
Image: Sergey Novikov (Shutterstock)However, what is possible, is to calculate bank fluctuations (i.e. winning and losing sequences).
With the help of knowing the best and worst case scenarios you can determine the ideal starting bank for any betting system of your choice.
At the end of the article you will find a few useful exercises to practise, with the solutions available as a free download to all of you who would like them.
Length of Winning and Losing Streaks
It stands to reason that the smaller the probability of an event occurring (i.e. higher odds), the longer the likely losing streak will be (in between winning bets).
However, the big question is how often and for how long will the losing (and winning) streaks transpire?
It is possible to mathematically calculate many things with statistics, including streaks of luck and bad luck. However, it is important to note that no matter how accurate the results may appear, they are ‘models’ (a formal representation of a theory).
In this article, we are talking about probabilities; what can we ‘predict’ about how things may develop in the future. Please bear in mind that any such hypothesis is always a “could happen” not a “will happen”.
Of course, the larger the sample size (i.e. number of bets), the more likely the prediction is to be correct. But apart from the bookmakers themselves, who else has a betting portfolio comprising thousands of bets every weekend?
Winning and Losing Streaks Formula
The longest expected losing streak (or winning streak) can be calculated using the following formula:
n = number of trials (i.e. total number of bets)
ln = natural logarithm1
P = probability2
| .. | = absolute value or ‘modulus’
1Suffice to say, explaining what natural logarithm is would be worthy of a series of articles. For the time being, use Excel to calculate this for you.
2For winning streak calculations use the positive value (i.e. the probability of winning). For losing streak calculations use the negative probability value. For example, if the probability to win the bet is 33% then the probability that the bet loses (negative probability) is 67%.
In practice, the formula is best applied to situations where you constantly bet repeatedly on the same probability, for example, on ‘red’ at the roulette wheel: its probability remains exactly the same with every new spin of the wheel.
For football betting the concept is much more difficult to apply as each bet is likely to have a different probability (e.g. one Over 2.5 Goals bet with a 55.3% chance, and the next with a 62.1% chance, etc.).
However, you can group bets in probability clusters – for example, bets with a 55%-60% expected hit rate, bets with a 60%-65% expected hit rate, and so on.
 Longest Winning and Losing Streaks, depending on the number of bets (Examples for 50, 500 and 1,000 bets shown)
Longest Winning and Losing Streaks, depending on the number of bets (Examples for 50, 500 and 1,000 bets shown)The tables above show the calculations of the expected maximum number of winning and losing streaks, depending on the expected hit rate (probability of the bet to win).
To read the tables, let’s explain the 70% line (odds in the region 1.4 and 1.45); in other words, bets with a 7 in 10 chance of winning.
The table on the left calculates the expectations of 50 tries (50 bets in a row, one after the next). You can see that the player will experience at least one streak of three lost bets in a row somewhere in the sequence.
On the other hand, he can expect at least one series of 11 winning bets in a row during the same sequence of 50 bets.
In contrast look at the 30% line (odds in the region of 3.2 to 3.4). In a series of 50 bets the bettor must expect at least one sequence of 11 consecutive losing bets, but will probably see only one set of three consecutive winning bets.
To develop a sense of probabilities and sequences, you can experiment with a dice. It has six faces; in other words, a probability of 16.67% (1 in 6 chance) of successfully landing on a chosen number.
Choose a number and count the number of throws until you succeed to roll it. Count also the number of consecutive successful rolls.
Choose two numbers that you do not want to roll (e.g. 5 and 6).
This means you have a 66.67% chance that one of the remaining four numbers is rolled.
In football betting terms, this equates to wagering on something like the full-time ‘Under 3.5 Goals’ market at odds of 1.50. (This experiment is just a little faster than waiting for 50 games to finish!)
Take a pen and paper and record 100 throws of the dice. If one of your four chosen numbers arrives mark a 1 on your paper; if the 5 or 6 are thrown, mark a 0. Count the number of winning and losing streaks you experience.
What is the maximum number of winning and losing streaks you experience in a sample size of 100 throws (bets)?
Having learned how to calculate the expected length of winning and losing streaks, the next question to ask is:
How many bets is it likely to take before I encounter ‘X’ losses in a row?
Timing of Winning and Losing Streaks
This formula is actually very simple:
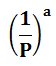
= 1 divided by P, to the power of a
P = probability (expected hit rate or loss rate)
a = number of won or lost bets in a row
In the tables below you can see how many attempts (bets) it needs to experience a specific, expected length of luck or bad luck. Again, the assumption is that the bettor bets all the time on the same probability:
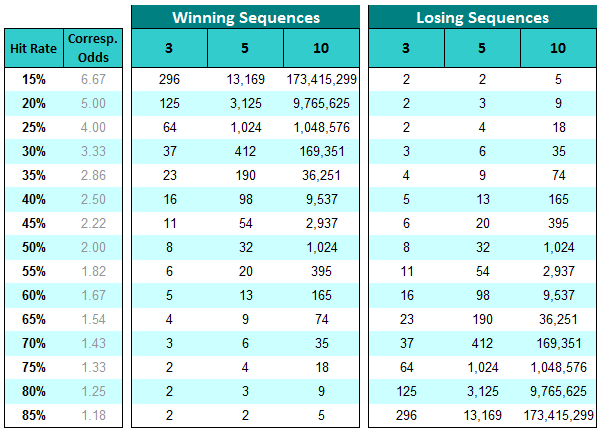 Expected time of occurrence of winning and losing streaks, depending on the hit rate
Expected time of occurrence of winning and losing streaks, depending on the hit rate
Reading the table:
Looking firstly in the right-hand column at the Losing Sequences, if the expected hit rate is 45% (what you should ‘expect’ at odds of around 2.2), then it is likely that you will experience a sequence of three losing bets in a row by the time your sixth bet is settled.
After 20 such bets it is likely that you will have seen a losing streak as long as five bets in a row.
Looking at the Winning Sequences column: you will win three times in a row at some stage during a series of 11 bets.
However, winning five in a row may only be seen once in every 54 bets.
As we mentioned before, in football betting it is extremely difficult, if not impossible, to find bets, all with the same probability of success.
However, you should at least try to understand the theory behind winning and losing streaks, as it will be easier on your nerves when you do encounter the inevitable run of bad fortune.
In particular, a thorough understanding of losing streaks is of enormous importance when setting both the size of your starting bank and stakes per bet.
Example:
A bettor prefers bets within the odds range of 2.0 to 2.5 with a hit rate between 40% and 50%. He plans to place 50 bets (e.g. two bets per round on 25 rounds of matches).
After looking at the tables, he knows that the maximum losing sequence expected is likely to be as long as six to eight lost bets in a row. Therefore, he knows that there may be at least one sequence of three or four consecutive rounds (weekends) when all bets lose.
After every 5th to 8th bet, he is also aware that he is likely to experience a loss of three consecutive lost bets (e.g. one weekend loses both bets, the following weekend only one loses).
He also knows that every 13 to 32 bets there will even be a streak of five losing bets in a row.
The bettor is fully aware that he has to take this into consideration and plan the starting bank accordingly to be able to ‘sit through’ these losing streaks.
Of course, he also knows that winning sequences will arrive too. In his case, with some ‘luck’, he may experience a winning sequence of five bets in a row after 32 bets. Every eight to 16 bets he will have a ‘lucky’ streak of three wins in a row.
This is certainly quite a fluctuation. When these ‘bad luck’ and ‘good luck’ streaks actually happen, nobody knows. However, what we do know is: They will happen!
Starting Bank – Rule of Thumb
A starting bank should be approximately five times the maximum expected losing streak. The reason for this is that a losing streak can happen right at the beginning, immediately followed by another bad run of luck. We are talking statistics here!
So if a bettor wants to stake 10 units per bet, the starting bank must be nine times (expected losing streak) the stake of 10 units multiplied by five = 450 units. Then he can risk 2.2% of his bank each time he bets (10 divided by 450). If losing, the stakes will remain constant at 2.2% and, if winning, raised gradually.
Questions to ask before setting the starting bank:
- What hit rate is expected (probability to win the bets)?
- How many bets are planned for the season?
- How long will the longest losing streak be?
- What is the desired stake per bet?
Calculation of the starting bank:
Exercises: Losing & Winning Streaks
- A bettor pursues a strategy with a win probability of 60% per bet (e.g. Under 3.5 Goals). He places one bet after the other; in other words, he waits for the outcome of each bet before placing the next. In total he places 50 bets.
What is the longest ‘losing streak’ (bad luck) that he can expect? How long is the longest ‘winning streak’ (luck) that can be expected?
- Same example as in (1): A strategy with a probability of 60% per bet; placing one bet after the other.
This time our punter is hoping for a ‘winning streak’ (luck) of 5 consecutive wins. How often does that happen?
- A gambler pursues a strategy with a probability of 20% per bet (e.g. ‘betting on the underdog’). Again, he places one bet after the other.
With a total of 500 bets, how long is the longest ‘losing streak’ that he must expect? After how many bets can he expect the longest ‘winning streak’?
- Same example as in (3): Strategy with a probability of 20% per bet; placing one bet after another
The bettor was hoping for a ‘winning streak’ (good luck) of five consecutive wins. How often does that happen? After which bet number should he expect ‘bad luck’ of five consecutive losses?
- Following the above two strategies (one with a 60% chance to win, the other with 20%) our bettor stakes 10 units per bet.
How high should the starting bank be for the 60% strategy, and how much for the 20% strategy?
Note: The initial bank should be approximately five times the maximum losing streak based on a total of 500 bets placed.
Answers to the Exercises
Just click on the button above and click on “Proceed to checkout” button in the new tab, then enter your name and e-mail address. Our automatic service will then deliver the file to you via e-mail, free of charge. The size of the PDF file is 320KB.
Optimising Your Bankroll
The factor 5 used in this article to determine the betting bank is a risk variable for risk-averse bettors. It is also the factor advisable for strategies with a 45% to 55% win probability (odds between 1.8 and 2.2).
Here is another article: How to Calculate Losing Streaks & Optimal Bankroll in which we provide a more detailed account of setting the ideal starting bank.
Risk management in sports betting is the foundation stone upon which all of your betting transactions should be built.
Risk management encompasses risk assessment, risk control and capital requirements, all of which cannot be addressed until you understand how winning and losing streaks are likely to impact upon your starting bank.






Hi
Just wanted to say a big thank you for creating this webpage (science-calculating-winning-losing-streaks) and detailed explanation – I’ve bookmarked the page!
I’ve googled long & hard for a laypersons explanation of win/lose sequences before I found this. I have no understanding of logarithms but this explanation allowed me for create Excel formula for my own strategies so it’s much appreciated :>)
You are very welcome, Tom!
Thanks for your interest in Soccerwidow.
Best of luck and regards.
Just want to thank for your articles and website. So well prepared and a really good approach to the whole betting thing. i look forward to order your course soon and learn more!
The two formulas you present must have an assumed probability associated with them. For example, the longest expected winning streak is abs(ln(n)/ln(P)). What is the probability associated with “expected” in this case? What is the probability a winning streak exceeding that number is experienced? Or the probability that a winning streak of that length is not achieved?
Similarly, for your “How many bets is it likely to take before I encounter ‘X’ losses in a row?”, what probability is implied by “likely”.
Thanks!
With our True Odds & Value Detector you can calculate the likelihood (probability) of an event happening, e.g. the team to win or to score in both halves, etc. In my book Fundamentals of Sport Betting, I explain more about odds calculation and how to calculate the ‘expected’ probabilities of Over/Under goals.
That should have answered your question: What is the probability associated with “expected” in this case? Look also through this website, I explain it in many articles.
Your other questions: What is the probability a winning streak exceeding that number is experienced? Or the probability that a winning streak of that length is not achieved? You can also ask: What is the probability to experience several times such a long winning or losing streak? – or – What is the probability to experience them several times in a row?
Toque, we are speaking here about probabilities, about something to be ‘likely’, never certainties… Of course, you can calculate that stuff but it really doesn’t make sense for any betting decisions. This article has been written to raise awareness for the length of winning/losing streaks.