Introduction to Combinatorics and Probability Theory
This article is a step-by-step guide explaining how to compute the probability that, for example, exactly 4 out of 6 picks win, or how to calculate the likelihood that at least 4 of 6 bets win.
To help your understanding of this topic you will need to comprehend the basics of football result probability calculations, which I explained in detail in the article Calculation of Odds: Probability and Deviation.
The Basics of Probability Computation in Football Betting
The following picks table contains 6 value bets including the calculated probabilities for each bet to win:
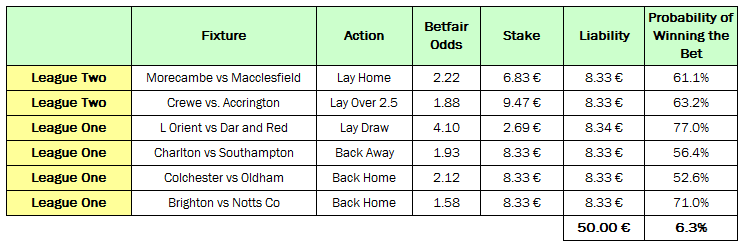
English Premier League - Example Picks 22.3.2011
Of the 6 published picks, 4 won and made a profit of 19.9% on the 50.00 € betting bank. I will now attempt to explain the mathematics behind the above selections.
The calculation of the probability that all 6 Picks will win is relatively easy and requires no knowledge of difficult formulas. You simply multiply together the given probabilities, thus:
The result of 6.3% is the probability that all 6 picks in the portfolio win.
Of course, the other end of the scale is that all 6 picks will lose. Again, this is a straight forward calculation: simply multiply the opposing probabilities to those used in the ‘win’ scenario, thus:
The result of 0.1973% is the probability that all 6 picks lose.
Summary:
- Probability that all 6 Picks win: 6.3%
- Probability that all 6 Picks lose: 0.1973%
If you divide 6.3% by 0.1973% the result is 31.93. This means the probability in this particular portfolio that all 6 picks win is almost 32 times higher than the probability that all 6 picks lose.
Practically speaking, there is a 32 times higher chance of winning all 6 bets and cashing 40.90 € profit than losing all 6 bets together with the entire 50.00 € starting bank.
Accumulated Betting Odds
- To win all 6 picks: 15.9 (1 divided by 6.3%)
- To lose all 6 picks: 506.7 (1 divided by 0.1973%)
These odds express that on average all 6 selected bets should win once in every 16 rounds and only once every 507th round should a total loss of the portfolio occur.
A single season’s football league betting will usually comprise approximately 80 rounds of matches (midweek and weekend betting). This means that statistically a total loss may happen once every 6.3 years betting on a similar portfolio to the example above each time. Of course, it could happen more often as wins and losses have a nasty habit of not lining up as cleanly as statistical theory says they should. For example, 2 total losses could occur in the first 2.6 years and then no more for another 10 years.
What is the probability that exactly ‘X’ picks win or lose?
Further interesting questions include what are the probabilities that exactly 5 of the selected 6 picks win, or at least 4 of the picks win, and following this, it is natural to ask whether it is viable to make long-term profit on this type of portfolio and if so, how much?
An easy starting point for assessing whether a portfolio is ‘worthwhile’ is by calculating the ‘expectancy’, in other words, how many of the picks are likely to win. This is simply the average of the win probabilities of the selected picks:
This value means that by betting on the above portfolio a success rate of 63.55% is ‘expected’, which would correspond to a hit rate of 4 from 6 picks (i.e. 6 [picks] times 63.55% = 3.81 [roughly 4 picks]). This means that on average this portfolio should usually bring around 4 successful picks. However, it is obviously necessary to check if the combination of 4 successful picks and 2 failed ones will produce a profit:
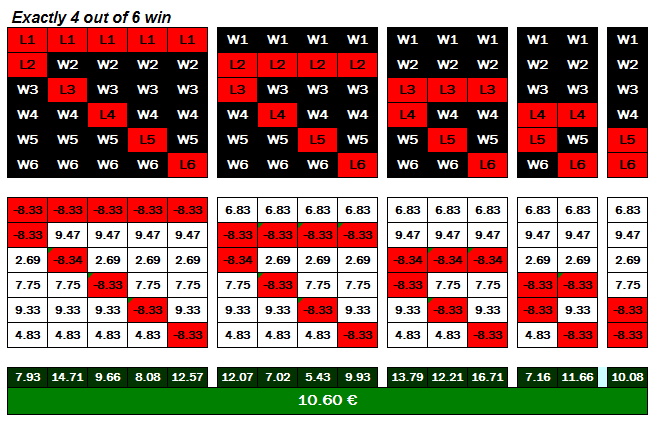
Profit Calculation: Exactly 4 out of 6 Selections Win
The above illustration shows that every combination of 4 picks from our 6-match portfolio would have returned a profit of between 7.02 € and 16.71 € depending upon the combination.
Important Note
Please note that the average value (expectancy value) does not mean a 63.55% probability that exactly 4 picks will win every betting round. The average value indicates that if you bet on this type of 6-match portfolio often enough, an ‘average’ of 4 hits can be expected.






Hey there, I was wondering, more the mathematical side of things, how would you work out the odds of say a 10 leg multi, with the options being head to head, Win/Lose (no-draw) situation?
So as opposed to the 3 choices in soccer (win,draw,lose) would you have more of a chance with for example tennis (win,lose)?
Hi Wade, combinatorics is a very wide field and to carry out quick calculations I recommend Wolframalpha. There you will be able to play through all kind of scenarios you can possibly think of.
Of course, I see.
But in this example you wrote, you showed a non “value” bets example (50%-1.90), and of course , in this case it’s nevermind you bet single or accumulator cause you had not the advantage!
But in the article you use 6 value bets. So simple bet the same 6 value bets as an 6/4 system bet not as 6/1. Of course you loose every time when you have 3 or less hit, but when you have 4 or more hit, the profit much higher. So the question: Is it much profitable to create system bets or accumulators with value bets (and only value bets) than bet these value bets as single bets in the long run?
And another theoretical question: You use a value bet calculator to find value bets, I use another method, another person use another method, etc. There are several ways to find a value bet. But who decide which method is right? Is there a law (within probability or statistic) or something which differs the methods or show the right way? Or in this random process (betting prognosis) there are no such laws or methods which are right 100%, and only the results (hit rate or yield rate) justifies the methods?
Hi falconer, many roads lead to Rome. 🙂
There isn’t anything in life which has a 100% certainty. You can come close but never to 100%!
Therefore, whatever method of statistical prediction you use, only the results (hit rate, or yield rate, or comfort zone or, or, …) justifies the method.
Regarding accumulators, you only decrease your probability to win. If only one leg goes wrong you also lose the winnings for the bets you actually got right. If you want to play accumulators then play them as individual bets. This is how it works: Place the first bet… if it wins then use the winnings to place the second… and so on. Keep some of the winnings to yourself, and if at some stage one leg goes wrong you still have something left.
Hello!
If we do not bet these events as an each single event (like in the example) but for example a 6/4 system bet ( which contain a 15 4 fold accumulators) is the (event happennig hit rate) probability calculation the same?
But of course the profit/loss scale doesn’t the same at all, right?
Thanks!
The probability calculations are always the same, but you must not forget that the bookmakers have usually the mathematical advantage on their site. If you are playing accumulators you are not reducing their advantage.
For example… 3 bets with a ‘true’probability of 50%. The fair odds would be 2.0. However the market offers these three bets at odds of 1.9 (implicated probabilities 52.6%).
Your chances to win this accumulator are 50% x 50% x 50% = 12.5% (converted in odds: 8.0)
The bookmakers are laying this bet at: 52.6% x 52.6% x 52.6% = 14.6% (converted in odds: 6.85)
Can you see that you are buying this accumulator bet to a much higher price than the bookmakers have to pay out should you win?
It’s a numbers game for the bookmakers. Of course, you won’t be the only one who plays accumulators. Of course, there are occasionally people who win an accumulator bet, but more often they don’t. It’s all about the mathematical advantage! Otherwise bookmakers wouldn’t stay in business!
I would just like ask about Probability of Winning a bet. I can see there 1.58,1.93, 2.12,….
You write like this:
1.58 – 71%
1.93 – 56.4%
2.12 – 52.6%
Mine calculation
1/odd X 100 is %
1.58 – 63.3%
1.93 – 51.8%
2.12 – 47.1%
Did i calculate wrong or you write wrong?
The probabilities provided in the screenshot are not the “implied probabilities” (converted bookmaker odds). The shown probabilities are the “true” probabilities. Sorry, I didn’t explain it clear enough in the article.
You are correct, if you convert odds, then odds of 1.58 convert into an “implied probability” of 63.3%, and so on…
However, the prices (odds) which bookmakers publish are rarely the true probabilities (otherwise these guys wouldn’t make money, would they?). You have to calculate your own probabilities in order to recognise the bets which are worthwhile to bet on. I explain this in great detail in my course: Fundamentals of Sports Betting
Hi, a little investment of your time in understanding Kelly Criterion will give you the background to optimizing your bankroll what ever it’s size by giving you the optimal betting size based on your edge. Good luck
Please help me clarify this.
If i theoretically and continuously bet at the odd of 1.9 on every game with a 10% over-round; and i win usually between 54% to 57% of my bet on the long term (above 1000 bets – that i consider long enough, statistically speaking). Using a sensible betting bankroll and stake that can withstand highest losings sequence.
NOTE: i do not consider calculating odds to check for value.
Do you consider me betting on Value? If yes, can we have another explanation of value betting depending on performance of the bettor or system if successful in the long term. Am not so sure if my question will hit the nail where i want it but if am successful in the long run is it because am betting on value (even though i unconsciously don’t look for it) or my accuracy rate gives me enough winning percentages to be profitable in the long run?
Thanks for your articles – so much value in a single place. Well done
Yes, if you have found an edge (mathematical advantage), then your are betting on “value”. It doesn’t matter how you found the edge.
Odds calculation helps to understand what is going on, and find the edge, but there are certainly people around who can do it without knowing anything about odds calculation. Some people are born with a great sense of probabilities, but they are rare.
Therefore if your accuracy rate gives you enough winning percentages, then congratulations!
Thanks for this great article, I haven’t finished reading it but I think it’s great. I always win by simply researching deep on a team and also using my instincts. Just two days ago I predicted 14 results (accumulators) which included Matchbets, that was awesome e.g. the Europa final, I just entered BTTS+2.5o. Then on online betting just placed a bet when Liverpool were leading at half time for a Sevilla win, the odds were crazy and tempting. I smashed the jackpot …. my best night so far. Research and Instincts.
Nonsense indeed.
What about the probability that they tie in which case you still lose your bet?
Hi Xy, of course, some bets will lose, some bets will win. There is no picking system where every bet wins. This doesn’t exist!
You may find following article useful: Probability, Expectation, Hit Rate, Value, Mathematical Advantage: Explained
Hi Soccerwidow,
Not sure if this blog is stil active or anyone following this.
I would like to liaise with Mohamed on his strategy. My email adres is vincentrichter[at]yahoo[dot]com
In a nutshell I have been playing and building on a system in the idea that Mohamed is thinking. Can you please put me in touch with him?
If there’s anyone thinking in this same line, drop me a mail!!
Thank you!
Hi, as confusing as my qstion may be I ll try my best to make it clear..i ve been looking for a way to play a risk free bet..a way I can play all the possible occurence in a bet and one outcome will win…I decided to go with the goal goal and no goal goal option in football betting..i also decided to go with10 accumulated bets in each ticket,i ll play as many ticket as possible with different occurences..plz I ll like to knw hw many tickets I m supposed to play in a 10 match accumulator to ensure that one of the tickets wins
Hi kingsley,
what you are talking about is called “permutations” – the act of arranging all the members of a set into some sequence or order.
The good news is: it can be calculated. Unfortunately, the bad news is: the topic and formulas cannot be explained in a short reply.
For a start, check Wikipedia, or simply google “permutations”.
Hello SoccerWidow, I love Excel and I like to read you site. I would like you to help me in a formula. We have 1-x-2, when we pick the dutch 1x , for example, that is a combination of the 1 and X odds. What is that formula so I can put in my excel?
Best regards
@soccerwindow
Dont consider the odds because odds are there to confuse us more.
On a personal opinion (Home/Draw/Away) have equal chances i.e 33% simply because the game has not been played yet. There is no way a team can have a higher probabality than another.
Hello Guys i have been betting for the last 6yrs and i came up with an idea. In soccer, when you are betting 1 match the outcomes are 3(Home/Draw/Away) so when you decide to choose an option (Home win) chances of you winning is 33% and the house is 67% irrespective of the odd.
And when you betting 2 matches in a combination bet there are 9 outcomes(Home/Home , Home/Draw, Home/Away ,,Draw/Home, Draw/Draw, Draw/Away ,, Away/Home , Away/Draw . Away/Away)
If you choose 1 option that is Home/Home chances of you winning is 1/9*100%(11%) and the house is 89% hence the reason for us loosing.But if you play 5 options out of 9 outcomes then you have a chance of winning 55% thats better than 11% .
Hi Mohamed, betting would be soooooooo easy if the probabilities for each outcome (home/draw/away) would be always 33% each. Unfortunately this is not the case.
Here is some reading on Probabilities, Expectations & Hit Rates
Sorry to disappoint. 😉
Adam,
0 Draws = multiply the chances that each game will not be a draw. In other words, if Game 1 has 29% chance of a draw, then it has 71% of not being a draw. Just multiply all these latter percentages together.
For one draw where Game 1 is drawn, multiply 29% by the remaining percentages of games not to draw, and so on.
Page 4 of this article shows how to construct a table using 4 from 6 as the example. Just follow the same structure and scale it down to your needs.
All the best.
Hello. I’m trying to find the probabilities of how many of 5 soccer matches will end in a draw. The possible outcomes are: 0 draws, 1 draw, 2 draws, 3 draws, 4 draws, 5 draws
Game 1 (based on draw odds): 29% probability of a draw; Game 2: 31% probability of a draw; Game 3: 31% probability of a draw; Game 4: 29% probability of a draw; Game 5: 31% probability of a draw.
I understand that multiplying all those percentages together gives me the probability that all 5 will draw, but I’m not sure how to calculate the probability for “0, 1, 2, 3, and 4” games that may end up in a draw.