Judging purely from statistics, watching French league games must be rather boring as there are never many goals.
 Image: koya979 (Shutterstock)
Image: koya979 (Shutterstock)The Dutch, on the other hand, tend to have at least five goals in nearly 10% of their matches.
From a betting perspective however, the French league is a more sound proposition because its results are statistically more reliable and predictable.
In this article we explore the ‘Goal Habits’ of four major European leagues and compare them using “simple” line graphs.
Goals Galore – Distribution Graphs
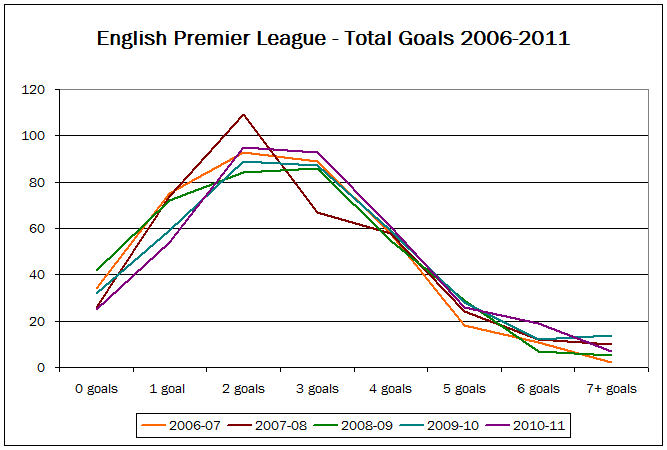
English Premier League: 20 teams; 380 games per season
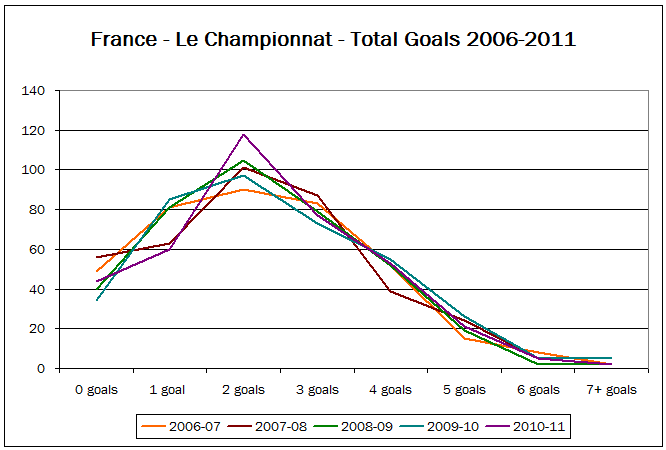
French Ligue 1: 20 teams; 380 games per season
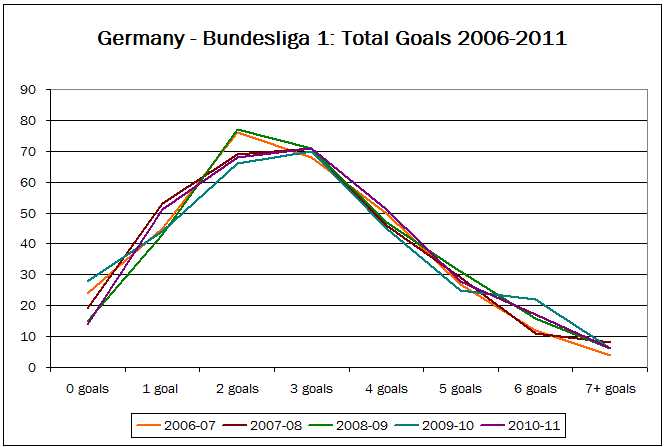
German Bundesliga 1: 18 teams; 306 games per season
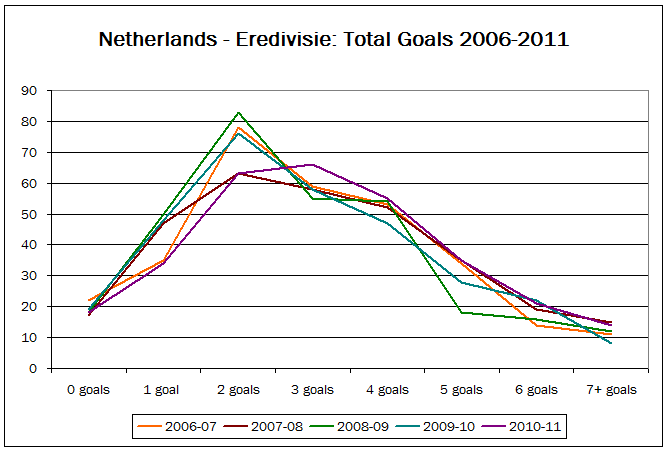
Dutch Eredivisie: 18 teams; 306 games per season






Thank you for sharing this article. So in an attempt to be more practical. Assuming we detected that under 1,5 goals has an average of 9% success with a deviation of +-1,5%. That would mean the range should vary from 7,5% to 10,5%. How could we build our portfolio? Take the worse scenario of 7,5% which means we need a minimum odds of 1/0,075 equals 13,33. But who can guarantee that we will get these odds from the bookies?
Hi betakos, there is no “guarantee” that you will get your desired odds from the bookies. If you use exchanges such as Smarkets then, of course, you can “ask” for your desired odds and hope that somebody matches your bet.
Do you know my course Fundamentals of Sports Betting – Over/Under X Goals? In part 2 I explain in great length how to utilise the knowledge of odds calculation, and with the cluster tables which come with the course I provide readers with a powerful portfolio betting tool for value betting.